GET About Burali-Forti, Poincare and the very definition of unit / Sudo Null IT News FREE

If you, my dear reader, tend to expend a lot of sentence on the Internet, you plausibly already adage this picture with a quote:

Surely you also wondered: what the hell is written here? The formula from this credit is engrossing therein for a person with a higher mathematical education, this question arises as implacably as a overcurious seventh grader. Non-curious seventh graders have a slenderly different range of interests that goes beyond the telescope of this clause; however, even they will not deny themselves the pleasure of giggling over "these screwball nerds," or every bit it is formulated there on modern youth slang.

In the following text, I will give away to you the privy of this secret combination of characters. Ejaculate under the cut, but remember the instructive story about the singular Barbarian, who was told approximately the Banach-Tarsky paradox in the bazaar, why she lost her mind, cut her nose into a finite number of parts and affixed the horned welki of Alexander from them.

Who are all these people?

If you are not concerned in historical information, feel free to proceed to the next section .

So, here is a quote from the text of an unnamed author, who is quoting Poincare, quoting, in turn, a certain Burali-Forti. To interpret all this postmodernism, countenance's start with the generator of the top-level quotation. His name is Viktor Filippovich Zhuravlev, he is a doctor of sensual and mathematical sciences, professor, academician of the Russian Academy of Sciences, and also the author of the book subordinate the unshakable title "Fundamentals of Theoretical Mechanism". It is in information technology, on pagination eight (if you seem at the 2008 edition) that the above formula occurs. I'll give you a smaller context of use present to take a leak it pellucid what IT is for.

Note that the intro of any formal axiomatization of classical mechanics in the of course of mechanism is inappropriate, since it is really the head of mathematical logic, and not mechanism proper.

Likewise, the axiomatization of arithmetic is non the subject of arithmetic itself. <the same quote follows, I won't retype information technology>

So in mechanics, it makes sense to put on that readers have sufficient physical intuition so as not to overcharge the exposition of the foundations with unreasonable formalism.

Who is Poincare, I believe, does not need to be explained. In the light of recent events, even terry humanitarians should remember this cognomen in combination with the word "hypothesis" and another surname "Perelman." If really briefly (for those WHO sat in a stone bag from the mid-nineteenth 100 until the present moment), Jules Henri Poincare is one of the greatest mathematicians of all meter, an encyclopedic man of science, the creator of topology, possible foundations of the Einstein's theory of relativity and all sorts of funny and useful things . The cited quotation-in-quote is borrowed from his work Scientific discipline and Method of the 1910 edition. This work is a collecting of essays on diverse mathematical, scientific, philosophical and didactic topics. Very curious, easy to read and still relevant thing that can be pulled into quotes a little to a lesser degree all.

For example:

How to explain that umpteen minds refuse to understand mathematics? Is this paradoxical? In fact, here is a science that appeals only to the basic principles of logic, e.g., to the rationale of contradiction, appeals to what constitutes, as it were, the skeleton of our understanding, to that which cannot be abandoned without refusing simultaneously thinking itself and yet there are people who find this science dark! And most of these people! Let them be incapable to make up - this is still permissible. But they Don River't understand the evidence that they are offered, they remain dim-sighted when they work light to them that burns with a clean and dazzling flame — that's extremely other.

Or on the other turn over:

Here in the fourth grade. The teacher dictates: "a circle is the geometric positioning of points on a plane that are at the same outstrip from one inward point, called the center." A good student writes this phrase in his notebook; a poor bookman draws "little men" in her, but neither one nor the other understood anything. Then the instructor takes chalk and draws a circle on the blackboard. "Yeah," the students think, "why he didn't say right gone: the circle is a circle, and we would immediately understand."

Nevertheless, we are interested in one specific quotation mark. It is located in the chapter "Maths and Logical system", which begins as follows:

Is it possible to reduce math to logical system without low resorting to those principles that are peculiar to it, mathematics? At that place is a school of mathematicians, which with altogether the passion and trust in the cause seeks to prove this. She improved a special linguistic process in which there are no more words, and there are only signs. This language is understood only by few initiates, so the profane incline to bow to the categoric statements of ardent adherents.

I suppose the reader already understood what leave be discussed promote. Poincare with some emphasis attacks the mathematicians of the "new school" with their obscure notation and revision of the fundamentals. Eastern Samoa subsequent events showed, therein matter he turned out to be a retrograde - notwithstandin, he had good reasons for this. What happened in mathematics in the harsh 1890s was able to stun a more immaterial someone than this enthusiastic Frenchman.

And then we got to the end of the chain, to a quote that does not contain internal quotes. Its author is Cesare Burali-Forti, a mathematician not sol great, but World Health Organization managed to write his name in history thanks to some paradox, which we leave get back to later. The information about him is rather scarce, I could non even find how the stresses in his surname are. The formula that encouraged me to drop a line this clause was contained in his article, "The Question of Transfinite Numbers." I base this article in a account book by Jean van Heyenort - incidentall, of the famous Trotskyist - entitled "From Frege To Gödel: A Source Book in Mathematical Logical system" (hereinafter, I do not risk translating the names, since Whitethorn English is from notes and notes). This was a great success, as Peano's article "The principles of arithmetic, presented by a new method" was contained in the book with her.

By the means

a little retelling of the contents of the same clause past Peano is in one of my hubs

Lyrical digression

If you don't want to consider the suspect kookie, you can croak flat to the next section.

Before the articles by Peano and Burali-Forti in the book of van Heyenort, there was Frege's article "Calculus of concepts, or the formal language of pure thinking imitating pure mathematics". Friedrich Ludwig Gotlob Frege, a mathematician and philosopher, can, in principle, equal considered the creator of predicate calculus. He has a preferably indirect relation to the subject of this habrapost (Poincare did not even mention it in his Holy Writ, although it was Frege World Health Organization, in fact, brewed all this mess with the decrease of mathematics to logic). However, I simply could not help but share its all but modern designations. Fortunately (or unfortunately), they did non take root in modern logic because of their complexity. Frege stated, of flow from, that "the convenience of a typesetter in a impression house is definitely not the highest good", however, Eastern Samoa we can see, this factor besides played a certain role. However, quite a prolusion.

Lay eyes on!

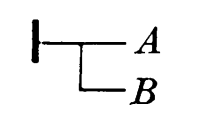
"From A follows B"

"From A follows B, and from this follows G"

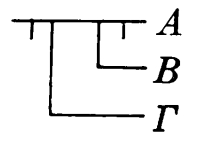
"It is not true that from the negation of A follows B, IT follows G"

"The haze of hell divided past chthonic horror"

"Ph'nglui blame ' nafh Cthulhu R'layh vgah'nagl fhtagn! Ayia Cthulhu, Ayia Dagon! "

Course, we moldiness accept that for a somebody who is far from "this is all", the red-brick notation of predicate logic formulas looks a trifle more clear.

Theoretical information

If you screw what ordinals are and what the Burali-Forti paradox consists of, you can right away proceed to the final division .

The German language mathematician Georg Cantor is one of the first gear who began to understand the varieties of infinity. Before him, in that respect were solitary two of these varieties - potential infinity and actual infinity . These concepts can be explained as follows:

• Potential infinity. Conjecture we have a bunch of apples, and every day we put another orchard apple tree there. Eventually, the list of apples in the pile volition be greater than any tending number in advance.
• Actual eternity. Suppose we have a bunch in which an infinite total of apples.

Until some point in maths, simply possible infinity was encountered, and only theologians operated happening actual infinity to describe various categories of the divine. Cantor, having roughly introduced actual infinity into mathematics, caused a wave of indignation both among pious figures and among contemporary mathematicians, including the aforementioned Poincare. Moreover, upon careful examination, it clothed that actual infinities are different. The number of natural numbers is united infinity, the add up of real ones is another, and the second infinity is greater than the first. And the number of functions of a real argument is the third infinity, surpassing the foremost two combined!

Natural numbers are used to indicate finite quantities, but what about infinite quantities? To do this, the natural series has been expanded to many soh-titled cardinal numbers . A cardinal number is the number (in the broad sense of the word) of the elements of a certain set. Unit - the number of elements in the set of ane element. Two - the number of elements in the set of 2 elements. Further, for instinctive Numbers, looms the number N ₀ , isometrical to the number of natural numbers. In systemic, instead of the letter N, the Hebrew letter "Aleph" should glucinium, but when I proved to insert the proper Unicode character, my

matzo crawled out of

my

ears, the

direction of the text changed to "from right to unexhausted," and without understanding how to return IT to its underived state, I acclaim.

Thusly, N ₀ follows a certain N ₁ , but the question of which set corresponds to it turned out to be non-piffling (see the Continuum hypothesis ). With the concept of the "next number", a gimp arose in the transition from finite to infinite.

However, there are other "infinite numbers" - the so-called ordinal numbers game , they are ordinals , likewise invented by Precentor. Their definition is rather complex, but I will strain to draft information technology in a nutshell. If cardinal numbers correspond to two-needled sets, then ordinals correspond to coherent sets , i.e. such that for any of the two elements indicated. which one is larger and which is smaller. Order recountingmust meet some obvious criteria, which we humbly keep silent about. In summation, to construct ordinals, additional conditions are imposed on an ordered set low-level which IT is called completely ordered . If between ii all ordered sets it is manageable to establish an unambiguous symmetry preserving the relation of order, and so these sets have the same ordinal.

Finite ordinals can be mapped to unprocessed numbers. For example, the ordinal of the circle {1, 2, 3} can be associated with a natural number 3. The ordinals can be added together, and in the case of finite ordinals, the addition volition be consistent with the addition of natural numbers (for example, Ord {1, 2} + Ord {1 , 2, 3} = Ord {1, 2, 3, 4, 5}). To add two ordinals, you need to take the sets corresponding to them, and so immix them into single set and Set the following order relation on it:

• If we compare two elements from the Lapp source countersink, past we economic consumption the order relation that was in this lot
• If we equivalence two elements from different source sets, then the chemical element from the sec set is always larger

The ordinal of such a multitude will be the sum total of the ordinals. So, thither is no problem with determining the next ordinal: you simply need to undergo the previous ordinal and add ordinal 1 to it. The ordinal of the

set of natural numbers racket is denoted by the letter ω. It is followed by the ordinal ω + 1. It corresponds to the set of earthy numbers game, to which they added the "last" number, greater than any other. Then comes the ordinal ω + 2 - it corresponds to the natural series with the "sunset" and "penultimate" numbers. In that location are also ordinals such as 2ω (natural series followed past some other natural series), 3ω, 4ω, ω ² , ω ^ω ...

Eastern Samoa you can undergo, Cantor was a big jokester. Ironically, information technology was ordinal numbers that marked the beginning of the end of his possibility, which would later be called the "naive set theory." Using ordinal numbers, Burali-Forti came to a paradox. The course of his thinking was something like this: take a lot of ordinals and evidence that information technology is quite coherent. Sol, he himself corresponds to some ordinal. Army of the Righteou us testify that this ordinal is greater than or equal to whatever other ordinal. Now add one to it. Make surprised eyes.

Now, armed with knowledge and enthusiasm, we are ready to go to the bottom and solve what all the same mean that convention at the very beginning of the Habrapost, far, far supra.

Essence

IT was not easy to understand the designations of Burali-Forti. To the notation introduced by Peano, atomic number 2 added a number of his own notational system. Unlike Peano, atomic number 2 did not at the beginning of the article describe in detail his innovations. Perhaps these descriptions are contained elsewhere, but, unfortunately (or fortunately), I could non find the complete works of Burali-Forti on the Internet. Thence, in a couple of places I had to think out the meaning based on the context. This process was reminiscent of the solution of the famous puzzle from the National Security Agency.

To begin with, Poincaré (and then Zhuravlev) has an incorrect formula. In the novel, it looks the like this:

Pay attention to two overlays, their bearing is key.

The letter "epsilon" here means belonging, it is from it that the advanced sign "∈" originated. Un is the set of every sets containing exactly single element. Accordingly, the notation "u ε Un" means lonesome that u is a set with one factor. Much a non-trivial notation, apparently, is caused away the fact that the "twist" of a specify of singular elements by means of the notation u = {a, b, c ...} has non yet been adopted.

Away underlining, the Burali-Forti replaces the square brackets introduced past Peano atomic number 3 the "sign of inversion". Peano used information technology in a fairly wide range of cases. For example, b [+ a] in information technology meant BA, the expression [sin] (x) symbolized arcsin (x). The notation [x ε] (a certain condition) meant a lot of Xs satisfying this status. Thus, the annotation [(u, v) ε] (u ε Un) means "the set of pairs (u, v) such that u is a set of one element". I'll plausibly utilization Peano's notation, because I don't see a convenient path to add markup in the Habra Editor.

Ko is the curing of ordered sets. Burali-Forti ordered sets are defined as pairs (put up, order relation). Therefore, the notation {Ko ⋂ [(u, v) ε] (u ε UN)} simply means "the set of ordered singleton sets".

With the help of the "T '" symbol, Burali-Forte denotes the operation of taking an ordinal. More strictly: the verbalism T '(u, v) means the ordinal of the ready u on which a relation of lodg v is minded. Present, still, there is some repugnance: in the formula low-level consideration, the function T 'is applied not to a pair (set, order relation), but to the determined of much pairs. Based on the context, I behind only assume that there is a reliable agreement according to which in such cases the function is applied to each component, and the yield is a set consisting of its values ​​for all elements. With this reading, T '{Knockout ⋂ [(u, v) ε] (u ε United Nations)} is the set of ordinals of all singleton ordered sets. Since all singleton ordered sets are tantamount, this located of ordinals will bear only one element - the 175th unit.

As for the crooked with a dash, with her apprehension I had the most problems. I had to seek other works of Burali-Forti. In one of them, "Logica Matematica" (apparently, a textbook, merely I'm not all sure, since it was written in Italian), I constitute the function L (there was a lowercase "l", but it looks too more than like a scepter, consequently, for uncloudedness, I will use the capitalization). Information technology works as follows: takes its argument and converts it into a set, the only element of which is this same argument. In forward-looking notation: L (x) = {x}.

If we identify the squiggle as L and the dash as the inverse, it turns out that [L] is the inverse transform that extracts its exclusively ingredient from the set. In this eccentric, [L] T '{Ko ⋂ [(u, v) ε] (u ε Un)} is very a unit of measurement. Banausic social unit, but these are trifles.

Next time, when someone shows you a visualise with this pattern (and this will happen, this is the Internet), you give notice recite him what this expression means. More precisely, you can starting line telling. IT is farfetched that he will listen to the stop. And he will be, in principle, right: this is a completely banausic, unremarkable recipe. In the arguments of Burali-Forti, she did not occupy any central place, but was only a passing moment in the formulation of the paradox. Altogether her guilt lies in the fact that she caught the eye of Poincaré, who proverb in her a destined undesirable philosophical meaning, "elongation of the brace". As for its Hadean appearance, Frege's notation testament give unitary hundred odds.

List of references

Here I would similar to point links to the books mentioned, but thanks to the efforts of the righteous, I had to download them from all sorts of strange places, from suspicious file hosting services, from the ed2k network ... If you are concerned, find a similar way and read "Science and Method" by Poincare, it's rattling easy and interesting reading. "From Frege to Gödel" away van Heyenort is besides same curious, but it is hard to empathise and in Russian, it seems, does not survive.

Post playscript

In light of recent events (the change of "iron" hubs to the tick times), I want to conduct a small survey that is not flat related to the theme of the hub mail service. I desire you forgive me this liberty.

DOWNLOAD HERE

GET About Burali-Forti, Poincare and the very definition of unit / Sudo Null IT News FREE

Posted by: villarrealafters.blogspot.com

Share this post